Robotics & Intelligence
Ranvit is a 20 years old undergraduate student from PSG College of Technology, Tamil Nadu, India. He intends to apply for a Robotics & Intelligent Systems major for his Master’s Degree.
Ranvit is a Head of Logistics Division in IEEE Student’s Chapter 12951 and a founding member of Artificial Intelligence and Robotics club at PSG College. He is currently undertaking a Bachelor Degree in Machine Learning and Tele-operation. His research paper on “Implementation of multi-agent mobile robot system for performing co-operative tasks “was accepted by the IEEE ISMAC 2019 conference.
University admission result
★ University of Maryland
★ Northeastern University
Scope of the program
Overall structure
Applying fundamental statistical methods to analyzing real-world data and relevant probability distribution modeling.
Learning objectives
- Introduction to R/Rstudio
- Data wrangling in R Downloading financial data from the internet
- Modeling probability distributions of stock and index returns in the US equity market
- Estimation methods for parameters (method of moments, maximum likelihood)
- Goodness-of-fit analyses for fitted probability distributions
- Analyzing the stability of fitted distribution models over time periods and the potential for regime changes
What challenges did he face?
- Even though Ranvit has good knowledge in Machine Learning, he needed a stronger portfolio to apply to his dream Master’s program.
How did our Robotics program help him?
- We set Ranvit up with the professor to work on data wrangling in R and to apply fundamental statistical methods to analyzing real-world data and relevant probability distribution modeling.
- Already with a good grasp of other programming skills, learning R language from the professor was able to take him higher academically.
- The professor agreed to provide a letter of recommendation for the student.
Student’s Testimonial
“The main objective of the program is to find the perfect theoretical mathematical model that best suits the empirical data and predict how good it would work with future data. For the first couple of sessions, I learnt a few basic tricks and how to work with R studio and R language, thankfully it was remarkably like Python language in which I have adequate knowledge. In a few other sessions, theoretical concepts behind the project were also covered.
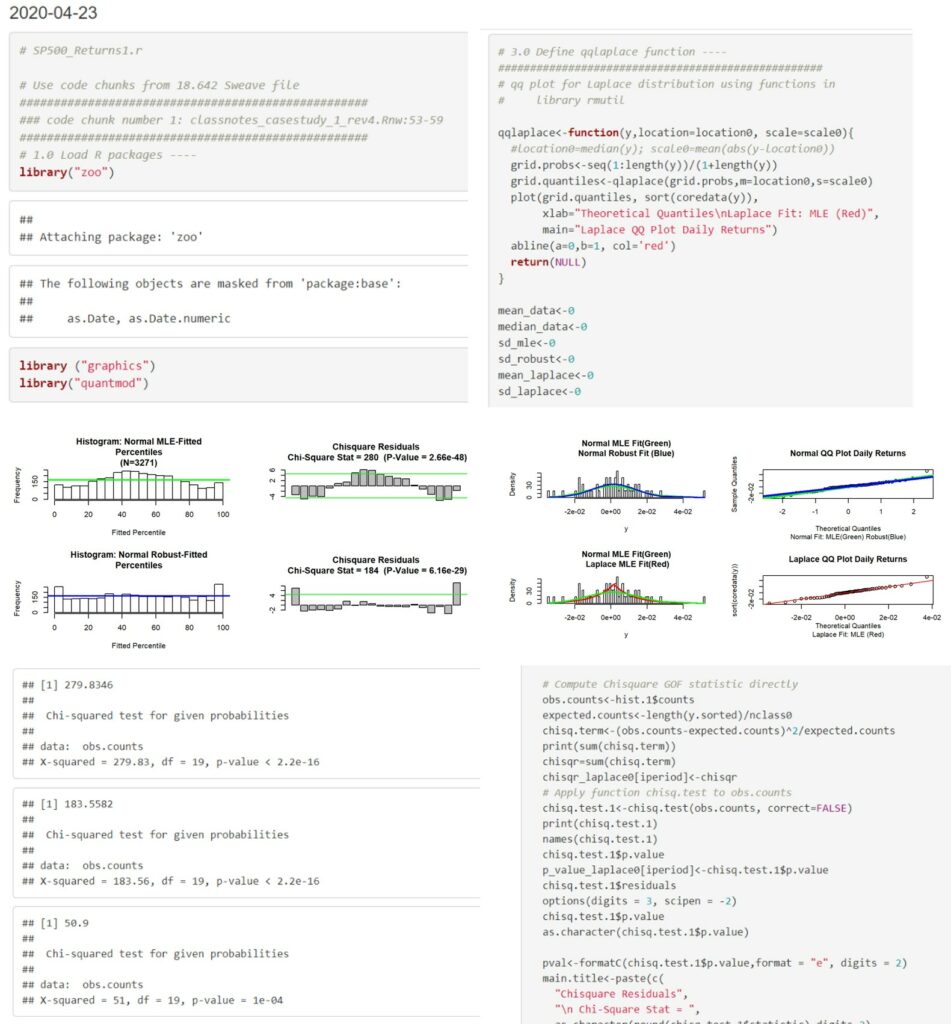
Firstly, stock data from various companies like Dell, Tesla, Facebook, Microsoft, Toyota etc., Bank of American Corporation, Treasury constant Maturity rate for 3 months, 1, 5 and 10 years through various timelines were downloaded using ‘FRED’. They were plotted daily wages were calculated and all those data were compiled into an R workspace. Using estimation methods like maximum likelihood theorem and method of moments, three distribution models namely Normal (MLE and Robust) and Laplace fits (MLE) were suggested by my mentor in his code.
The data from the previously created workspace was fed into this program to create QQ-plot and line plot whose output was the daily per cent returns and the Chi-square for each fit was also calculated and plotted alongside. The entire timeline was also broken into various small ones to check how each model worked with smaller periods. The stocks of Toyota Motor were chosen for the final analysis. Upon running the program, it was noted that the Laplace model performed better with longer periods whereas the Normal model was better with shorter periods.
One- another interesting find is that Normal Robust fit irrespective of any periods performed better across 5th to 95th percentile of the data and the Laplace model fits the peak value perfectly. Statistically speaking one neither eliminate any fit based on their p-value nor come to any decision blindly based on the results. If the p-value for a fit is higher it generally means that fit has less evidence and that particular fit is well able to match with the empirical data, it just helps us to judge the consistency of the fit.
To conclude with, during this intern I have observed that different models fit different percentiles perfectly, but overall Laplace model seemed to have consistency over others.“
Ranvit Rathore
Matched professor:
A Mathematics lecturer in MIT, the professor has been an investment manager, exploiting advanced statistical analytics to manage a variety of investment programs.
Recommendation letter
Based on your knowledge of this student, would you recommend this student to selective universities?
“Yes, I would strongly recommend Ranvit to selective universities for graduate programs involving quantitative/computational study.
Ranvit is extremely bright, thoughtful and analytical. He demonstrated a strong work ethic with proactive, self-motivated efforts. He has demonstrated high intellectual curiosity combined with effective, focused research work.“
Lecturer from MIT
Excerpts from the student’s work